Met enige regelmaat zien we prognoses voorbijkomen, die suggereren dat de oversterfte voorbij is. Telkens weer is dat op basis van het verkeerd samenvoegen van cohorten, waaruit vervolgens onjuiste conclusies worden getrokken.

Laat ons een voorbeeld geven, ontleend aan een rekenvoorbeeld dat een criticus ons gaf. Versimpelde cijfers voor een klein cohort van drie leeftijden met drie verschillende sterftekansen (10%, 20% en 30%). Een hypothetische situatie in 2019 en in 2024:

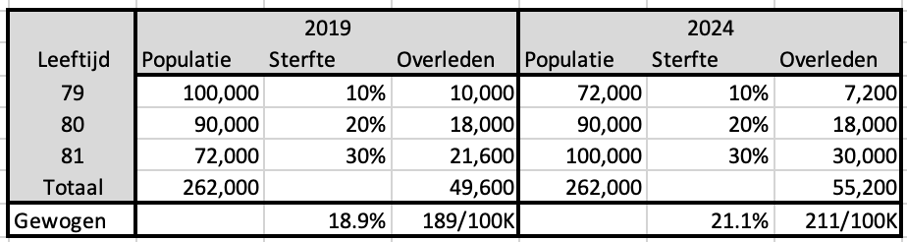We concentreren ons op de sterfte bij de 80-jarigen. Die sterftekans is 20% en daarbij maakt het niet uit of we in 2019 of in 2024 naar deze sterftekans kijken. In dit voorbeeld nemen we dus aan dat die kans niet verkleint door betere gezondheid of andere oorzaken. Op basis van die sterftekansen rekenen we ook het aantal overlijdens per leeftijd uit in 2019 en 2024.

Vervolgens nemen we aan dat we niet de beschikking hebben over de cijfers van 80-jarigen, maar dat ze alleen beschikbaar zijn als samengesteld cohort van 79-81 jaar. We schatten dan de sterftekans voor een 80-jarige als het gemiddelde van de 3 cohorten 79-81 jaar.

We tellen in 2019 dus 262,000 inwoners in dat cohort en totaal 49,600 overlijdens. Als we dat op elkaar delen, zien we een sterftekans van 18,9% en dat is flink minder dan de 20% die we zien bij de 80-jarigen. Alleen door het samenvoegen met de twee aangrenzende leeftijden.

In 2024 verwisselen we de populaties voor 79 en 81 jaar. We zien nu dus meer overlijdens dan in 2019, terwijl het totaal aantal inwoners en de sterftekansen hetzelfde blijven. De gemiddelde sterftekans van het cohort is nu juist hoger geworden. Dus de uitkomst van die sterftekans hangt af van de verdeling van de populaties binnen het cohort.

Hoe het hoort

In 2023 publiceerden we dit artikel: An analysis of excess mortality based on age and sex; the possible role of Covid-19…  Hierin beschrijven wij de rekenmethode gebaseerd op trends, die berekend worden op basis van de populaties en overlijdens, maar wel per leeftijd en per geslacht. Inmiddels is dit de basis voor wat we Normsterfte hebben gedoopt.

De berekeningen werden destijds gedaan met een lineair model, waarbij we er dus van uitgaan dat de daling (of wellicht stijging) van de sterftekans evenredig is met het jaar waarvoor we de verwachting berekenen. Voor een beperkte tijdspanne is dat nog wel in orde, immers de sterftekansen wijzigen maar langzaam. In tien jaar zien we een daling van rond de 20%. Maar eens zal de daling nog langzamer moeten gaan of wellicht zelfs tot stilstand moeten komen, we worden immers niet onsterfelijk. Daarom zijn de trendlijnen inmiddels vervangen door een exponentieel model. De verschillen blijken klein te zijn, maar toch…. Als voorbeeld de sterftekans op 50-jarige leeftijd:

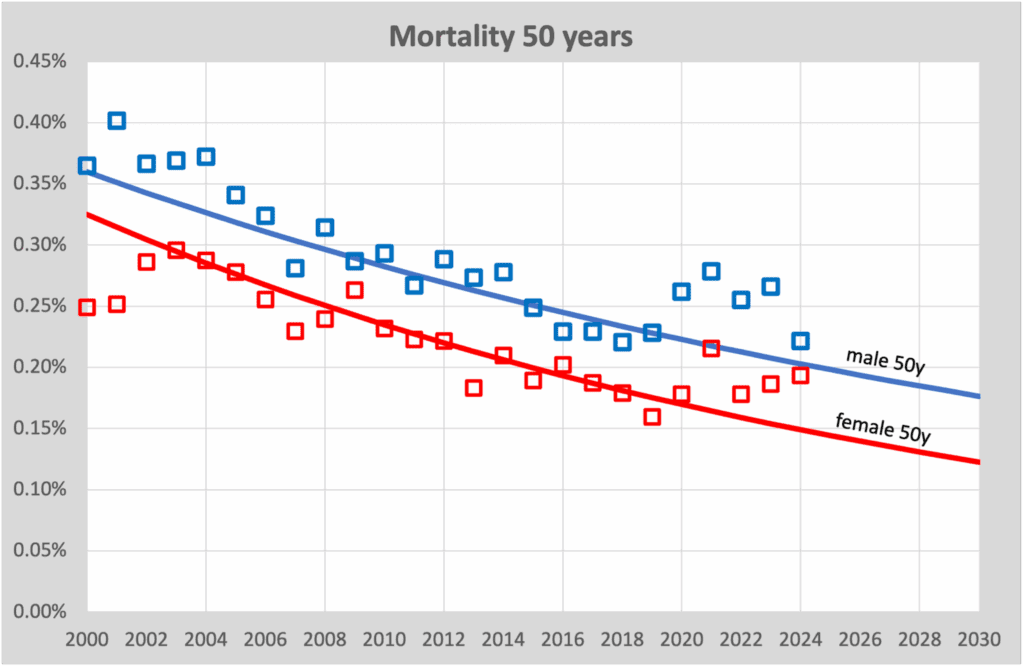We zien hier dat in de loop van 20 jaar (2000-2019) de sterftekans langzaam afneemt van rond de 0,35% in 2000 naar 0,2% in 2020. We zien ook dat de trendlijn ietsje kromloopt. Dat komt door het exponentiële model dat we inmiddels gebruiken. Maar het is minimaal. Belangrijk is dat we de sterftekans langzaam zien afnemen.

We moeten ons dus tegelijk realiseren dat deze grafiek een enkel leeftijdscohort is van alleen 50-jarigen. Vergrijzing van andere cohorten is dus niet van toepassing, dit gaat alleen over de overlijdenskans. Een tegendraadse trend want door vergrijzing stijgen de sterftecijfers van de bevolking als totaal, terwijl theoretisch elk 1-jaars cohort een dalende trend zou kunnen laten zien.

Alle leeftijden samen

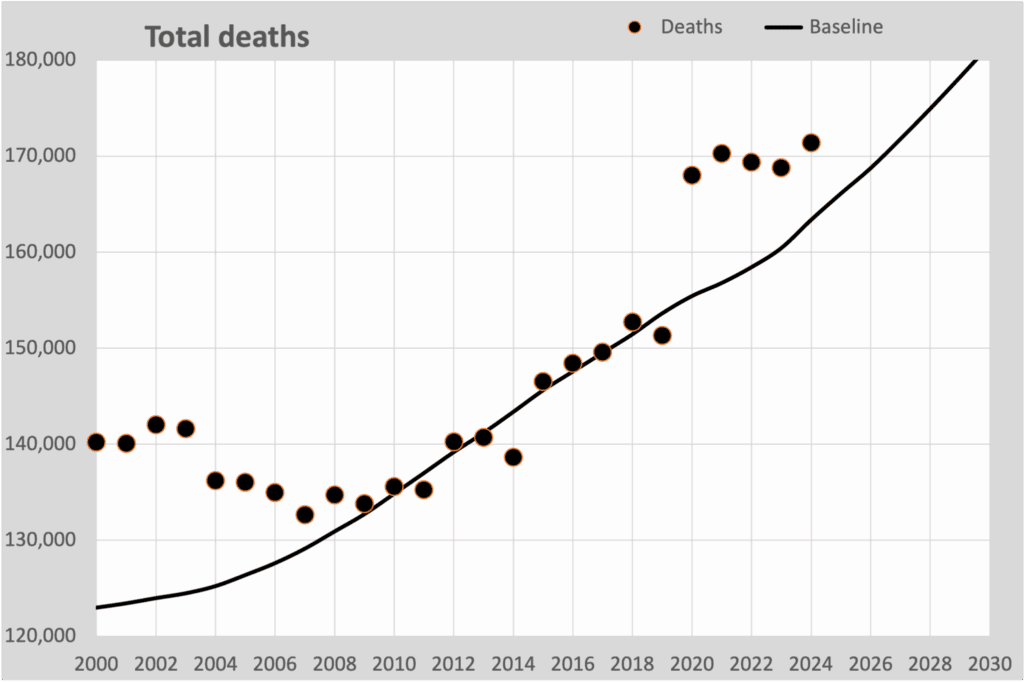We kunnen nu in één grafiek het totaal aantal overlijdens tonen in relatie tot de trendlijn van sterfte van 2010-2019. Dit is deze grafiek.

De zwarte lijn is berekend op de te verwachten sterftekansen op basis van alle 1-jarige trends 2010-2019. Die jaarlijkse sterftes passen dus mooi rondom deze lijn.

In 2009 was er een kentering in de afname van de sterftekans. Na een dalende sterftekans, vooral boven de 50 jaar, stabiliseerde de afnemende sterftekans tot ongeveer 1% per jaar. Dat zien we in deze grafiek terug: de dalende sterfte gaat over in een stijging door de vergrijzing.

Nu op basis van jaarcijfers per 100K

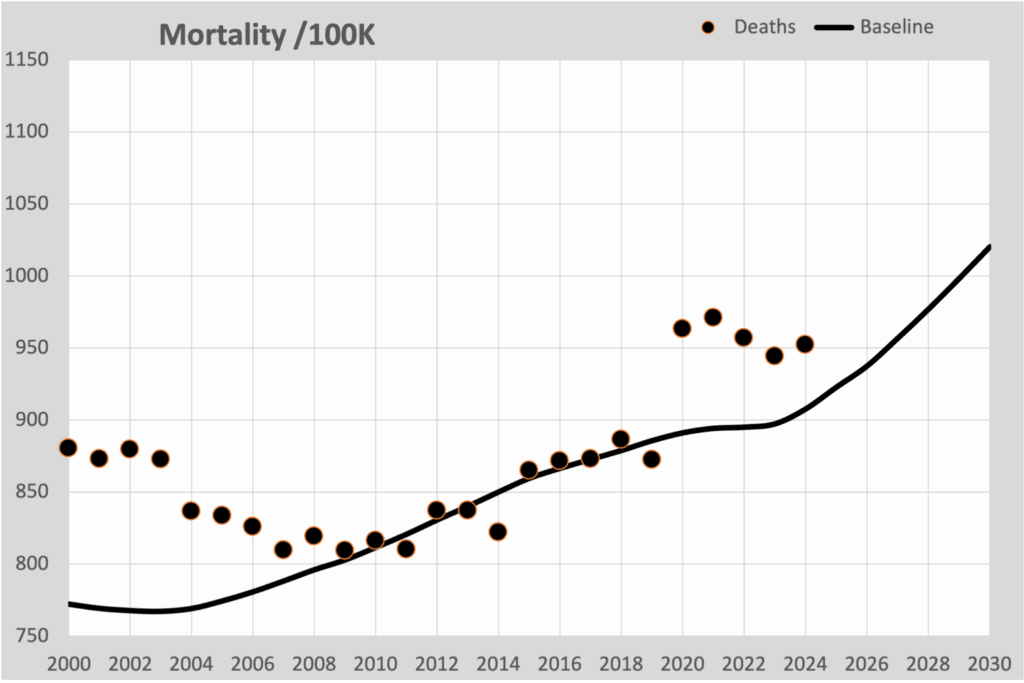In deze stap vereenvoudigen we onze rekenwijze, zoals door velen wordt gedaan. We gaan uit van de totaalcijfers per jaar en reken die om in sterfte per 100.000 inwoners, meestal afgekort tot “per 100K”. Deze grafiek ontstaat dan.

We zien dat de bolletjes ruwweg gelijkliggen in vergelijking tot de vorige grafiek en dat klopt. Voornamelijk is de schaalverdeling anders. Maar ook is de grafiek iets gekanteld, omdat de bevolking langzaam groeide. In 2019 waren er 10.000 meer overlijdens dan in 2000, maar uitgerekend per 100K was het vrijwel gelijk. De bevolkingsgroei en vergrijzing waren de oorzaak. Er waren 1,4 miljoen meer inwoners.

De getrokken lijn is weer dezelfde baseline als uit de vorige grafiek, wederom doorgetrokken tot 2030 met behulp van geschatte populaties na 2025.

Maar dan…

Foute modellen

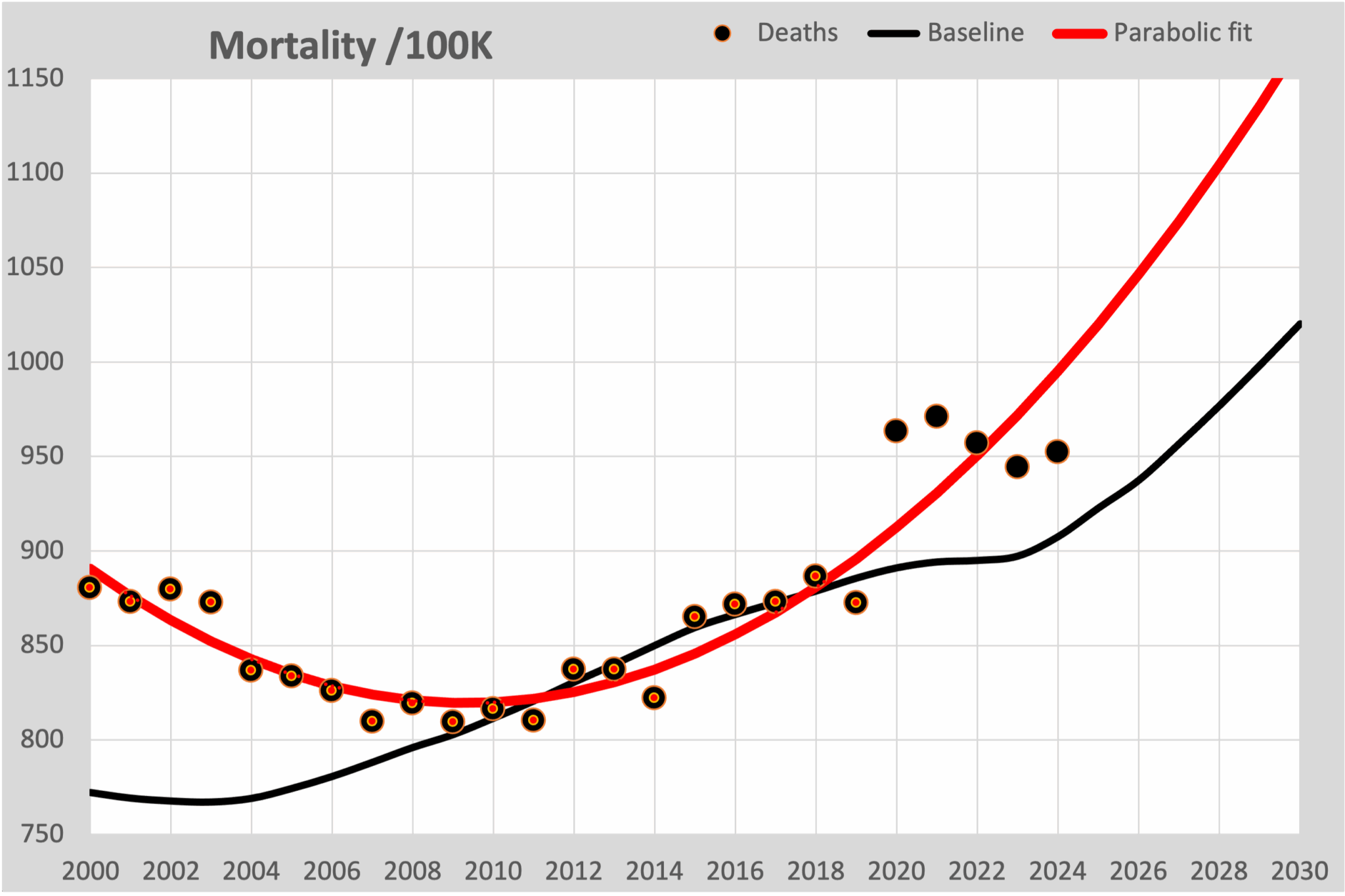
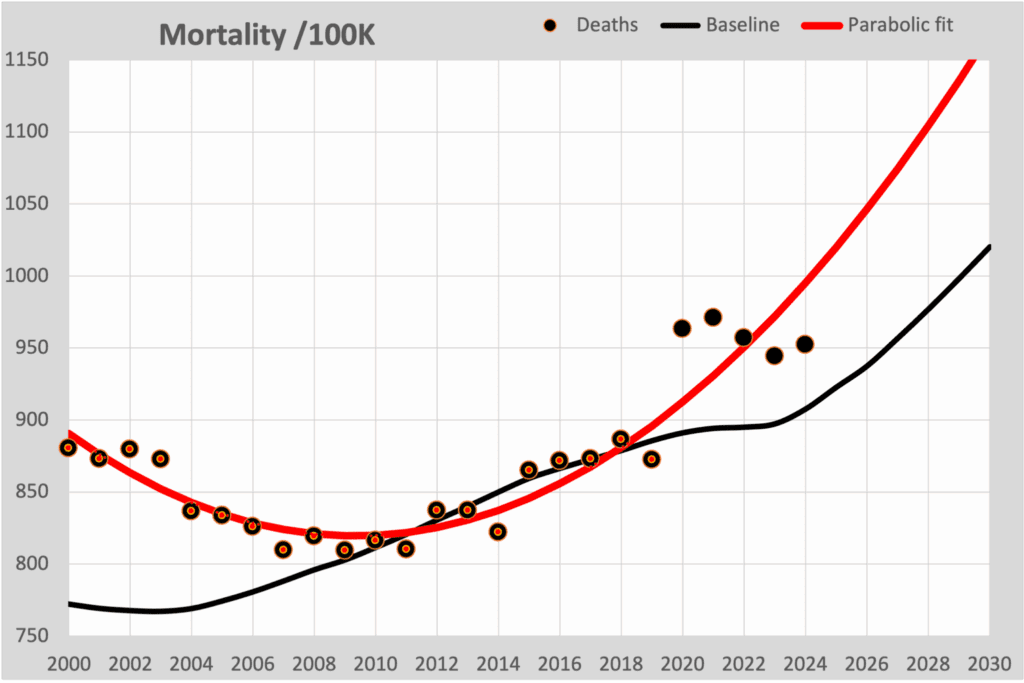Veel thuisrekenaars gaan ervan uit dat je door de 100K-punten t/m 2019 een curve kunt fitten, die het verloop na 2020 zal voorspellen.

In deze grafiek is nu de parabolische gefitte lijn rood ingetekend, zoals je die in veel grafieken ziet verschijnen. Hier gaan twee zaken fout:

1. De gefitte curve (ongeacht het gekozen model) volgt voornamelijk de cijfers die het gevolg zijn van de bevolkingsgroei en niet de verwachte sterftekans. De knik bij 2020 wordt zo gemist.
2. De dalende sterfte van 2000 tot 2010 laat hen verleiden te kiezen voor een parabolisch model, dat de cijfers ook vóór 2010 goed beschrijft. De consequentie is dat voor de toekomst dan juist een steeds sterker stijgende sterfte wordt voorspeld.

Het niet meenemen van de bekende cijfers voor bevolkingssamenstelling zorgt ervoor dat de lijn gedwongen wordt om die wijzigende cijfers te fitten. Het is dan ook een foute veronderstelling dat het omrekenen naar overlijdens per 100K van de bevolking dit effect neutraliseert.

Goede modellen

Omdat er nog steeds geen stabiele gezondheidssituatie is, moeten we een “best guess” prognose maken voor cijfers vanaf 2020. De prognose kunnen we grotendeel baseren op de bevolkingssamenstelling zoals het CBS die elk jaar publiceert. De grote onbekende is natuurlijk de te verwachten cijfers voor de sterftekansen. In ons rekenmodel gaan we ervan uit, dat de eigenlijk te verwachten sterfte een voortzetting is van de trend die we tot 2019 zagen. Ook het CBS heeft lang aangegeven dat zij volgens dat principe werken. De totaalcijfers van CBS en ons Normsterfte model kwamen tot 2022 dan ook heel goed met elkaar overeen.

Goede modellen gaan dus uit van individuele sterftekansen voor elke leeftijd en geslacht. Deze sterftekansen vertonen een ontwikkeling door de tijd heen. Het gekozen model bepaalt hoe goed de voortzetting geweest zou zijn als er geen “onverklaarde sterfte” geweest zou zijn. Het is ook nog onduidelijk of wat ons is overkomen sinds 2020 van invloed is op de sterftekans op de lange termijn. Het kan zelfs zo zijn dat er groepen mensen zijn die niet zijn getroffen door wat we nog steeds niet weten. Wellicht dat we daar in de komende jaren meer over leren.

ASMR

De ultieme manier om te corrigeren voor veranderingen in de bevolkingssamenstelling is de ASMR (Age Standardized Mortality Rate). Daarbij worden de sterftecijfers omgerekend naar een standaard bevolking. In ons geval kiezen we voor de bevolkingsopbouw van 2019, de laatste zonder invloed van de “grote onbekende”. Ook de baseline rekenen we op deze manier om naar de cijfers van 2019. Dit is de grafiek die daarbij hoort.

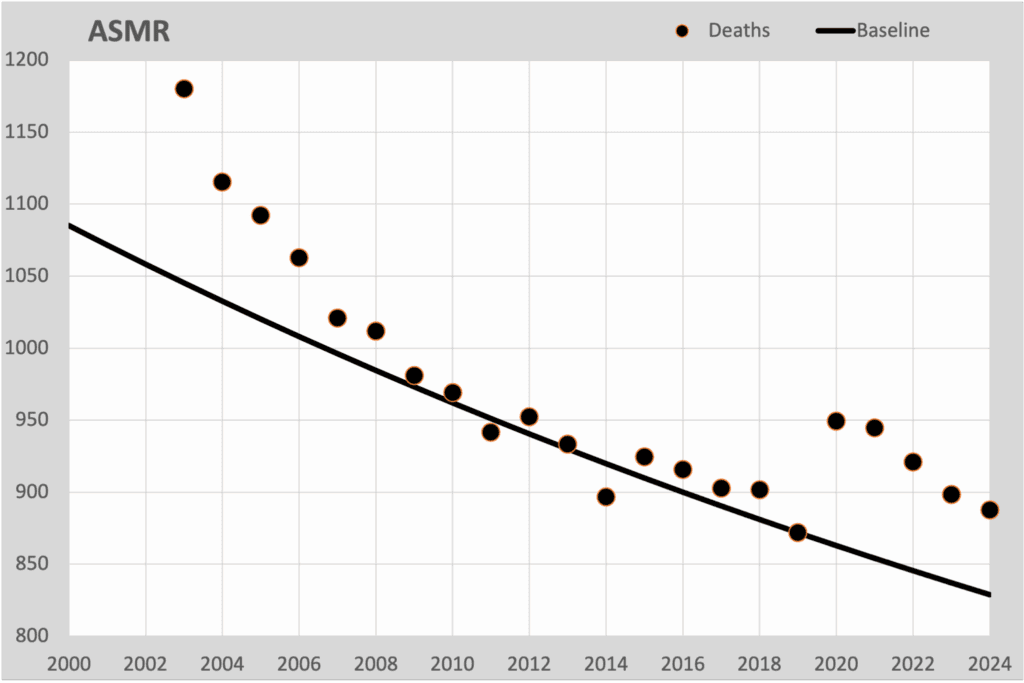Dit is als het ware de sterftekans als de bevolkingssamenstelling niet zou zijn veranderd, geen vergrijzing. Alhoewel we deze cijfers niet rechtstreeks kunnen vergelijken met de daadwerkelijke sterfte, geeft het wel een goed inzicht in de ontwikkeling van de sterfteverwachting. Net als bij de sterfteverwachting voor 50 jaar in de eerste grafiek ook hier dezelfde daling, berekend voor alle inwoners volgens de ASMR-methode. En het belangrijkste: hier zien we de oversterfte ontstaan vanaf 2020. Ontdaan van alle vergrijzingseffecten. Dus iedereen die vergrijzing noemt als oorzaak van de oversterfte, kan aan deze grafiek zien dat het niets met vergrijzing te maken heeft.

Keuze van historie en model

Een lineaire trendlijn is ongeschikt voor langere periodes waarin zelfs de zachtste kromming een steeds grotere discrepantie zal vertonen tussen verwachting en realiteit. Daarom hebben we nu gekozen voor een exponentieel rekenmodel. Dit veronderstelt dat de sterfte elk jaar met een vast percentage daalt.

Bij een langere referentieperiode wordt soms gekozen voor een parabool, die tot 2020 een daling en daarna een stijging laat zien. Wil je die curve ook verder in de toekomst kunnen volgen, dan staan er demografische onmogelijkheden in de weg, zoals een aanhoudende versnelling van sterfte, een onwaarschijnlijke ontwikkeling..

Toch laten ook de punten vanaf 2000 een duidelijke regelmaat zien die te formaliseren lijkt. De beste fit vinden we in een logaritmisch verloop, dat vrijwel naadloos aansluit bij de punten 2000 t/m 2019.

Het is goed verdedigbaar dat we deze lijn voorlopig kunnen doortrekken: hij leidt niet tot onmogelijke scenario’s. Sterker nog: hij verstevigt de validiteit van de exponentiële 2010-2019 lijn omdat beide lijnen vanaf 2014 nagenoeg gelijklopen.

Conclusies

De prognose voor het te verwachten verloop vanaf 2020 hangt sterk af van de keuze van het rekenmodel en de te kiezen tijdspanne waarmee het model gevoed wordt. We zien deze keuzemogelijkheden:

1. Lineair van 2010-2019. Gepubliceerd in Researchgate. Lijkt de te verwachten sterfte goed te beschrijven en geeft een prognose die goed past bij de CBS-cijfers.
2. Exponentieel van 2010-2019. Geeft vrijwel dezelfde cijfers, maar is iets realistischer op de langetermijn en dus iets beter.
3. Parabool van 2000-2019. Geeft voor de jaren 2000-2010 een betere beschrijving, maar voorspelt een sterke stijging vanaf 2020. Dat is een keuze, die niet aansluit wij de werkelijkheid.
4. Logaritmisch van 2000-2019. Een verloop dat niet door een fysische achtergrond wordt onderbouwd, maar wonderbaarlijk gelijkloopt met de cijfers van 2003-2019.

Concluderend: het rekenmodel dat uitgaat van een parabool als model, voorspelt een verloop van de sterfte die vanaf 2020 gedwongen wordt te stijgen. Ondersterfte vanaf 2022 is dan het gevolg. De andere drie modellen voorspellen vanaf 2014 allen vrijwel exact hetzelfde verloop. De eerste twee passen zeer goed bij biologisch verklaarbaar gedrag.  De laatste werkt ook zeer goed, maar is meer een optische en cijfermatige fit dan onderbouwd door demografie of biologie.