Verzekeraars zijn altijd druk met het zo nauwkeurig mogelijk berekenen van de pensioenpremie. De pensioenpot moet altijd in evenwicht zijn. Aan de ene kant komt er geld binnen via het werkende deel van de bevolking en aan de andere kant wordt het uitgegeven aan de pensioenen van gepensioneerden.

Bij gelijkblijvende pensioenleeftijd, moet er dus goed gekeken worden naar het te verwachten aantal jaren waarvoor pensioen moet worden uitgekeerd. Bij een pensioenleeftijd van 67 jaar en een levensverwachting van zeg 82 jaar, moet er dus gedurende 15 jaar pensioen uitbetaald worden en dat is opgebouwd in zeg 45 jaar.

Het goed kunnen bepalen van de levensverwachting is daarbij cruciaal. Als we opeens 1,5 jaar ouder gaan worden, moet er 10% meer premie opgebracht worden. Omgekeerd, als we 1,5 jaar eerder sterven, zou de premie met 10% omlaag kunnen. Daalt de pensioenpremie dan door modelleren?

Het CBS publiceert daartoe grafieken, waarin we deze levensverwachting kunnen aflezen. Zelf hebben we deze exercitie ook gedaan en komen uit op vrijwel dezelfde cijfers.

Ruwweg komt er elke 7 jaar een jaar bij in de levensverwachting. Betere medische zorg, vooral bij middelbare leeftijd, is de voornaamste reden van deze stijging. Tot 2008 was deze stijging sterker, kennelijk was er toen meer winst te behalen.

In 2020 zien we een plotselinge daling als gevolg van corona. Vanaf 2022 vindt er herstel plaats. Maar wat vinden de verzekeraars hiervan?

Is oversterfte verdwenen?

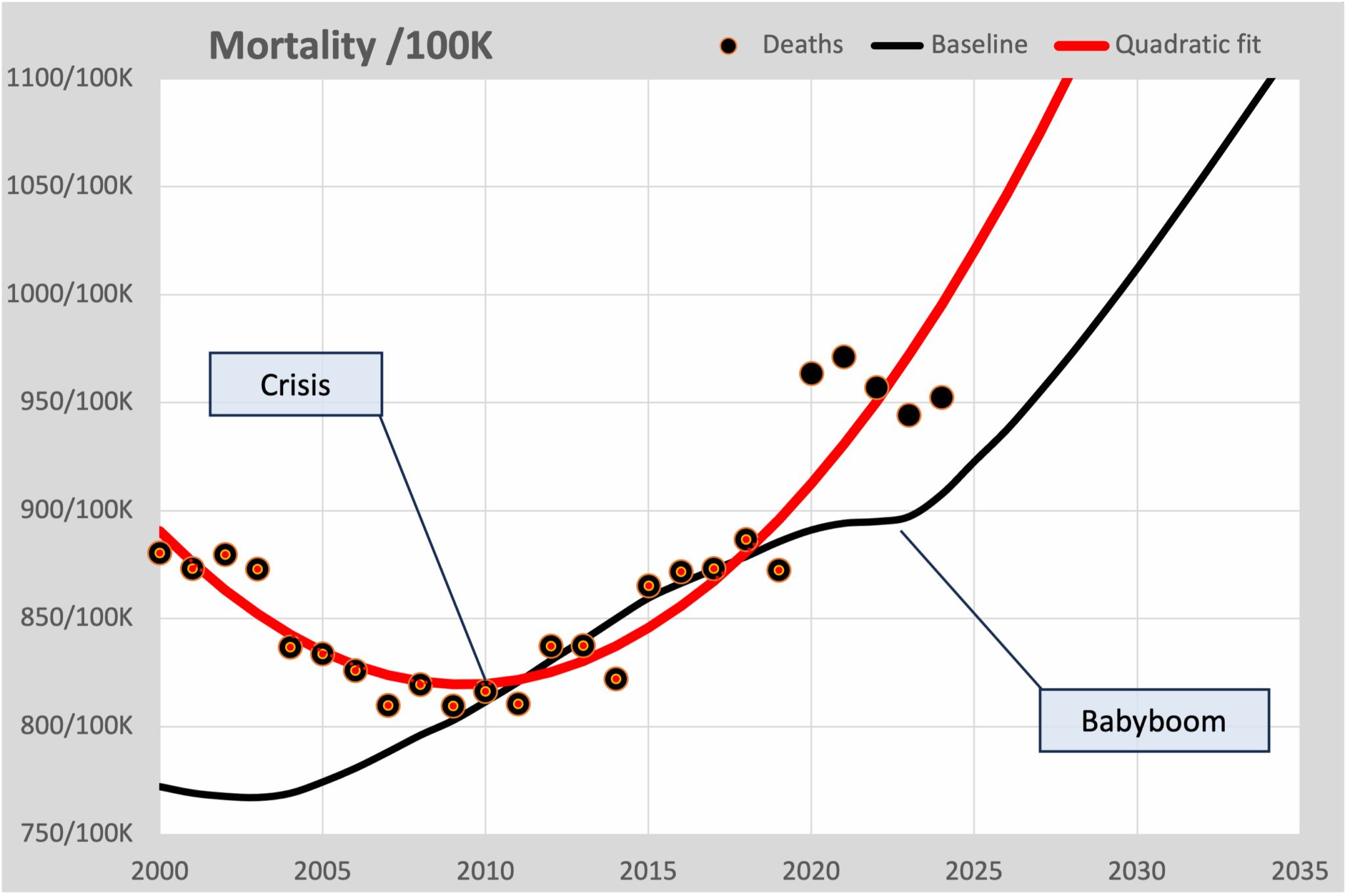
Er duiken steeds weer berichten op die stellen dat de oversterfte is verdwenen. Ook het RIVM suggereert dit met hun wekelijkse grafieken die telkens weer vermelden “Niet verhoogd”. Grafieken die we verder langs zien komen en zouden bewijzen dat oversterfte is verdwenen, zijn vrijwel altijd gebaseerd op kwadratische fits. We schreven daar dit artikel over: Foute modellen. Deze grafiek lieten we daar zien:

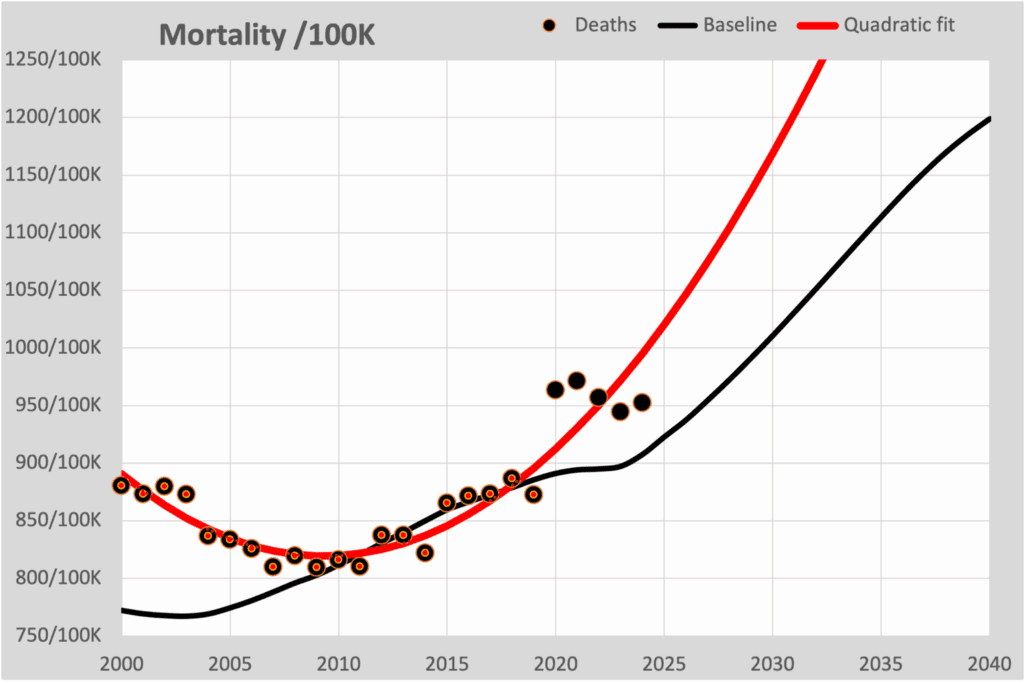De zwarte bolletjes zijn de werkelijk sterfte, uitgedrukt als aantal overlijdens per 100.000 inwoners. Dat is dus onafhankelijk van het aantal inwoners, dat voortdurend toeneemt. De zwarte lijn is de berekende sterfte volgens het Normsterfte model, dat een exponentiële lijn fit door de 10 jaren voorafgaand aan corona.

Het lijkt dan merkwaardig dat die sterfte toeneemt, terwijl de sterftekans voortdurend iets afneemt. Dat komt door de vergrijzing. Het aantal ouderen neemt in verhouding sterker toe in vergelijking met het aantal jongeren.

Maar eens zal er wellicht een stabiele bevolkingssamenstelling zijn, als we als Nederlanders vasthouden aan gemiddeld 1 kind per inwoner, oftewel 2,1 kind per echtpaar. In dat geval zal er jaarlijks ongeveer 1/85^e deel van de bevolking overlijden, als we ervan uitgaan dat we gemiddeld 85 jaar oud worden. Dat komt overeen met ongeveer 1200 overlijdens per 100.000 inwoners. Dat is dus ongeveer de bovenkant van deze grafiek.

We zien dat ook terug als we de zwarte lijn volgen. Die buigt al af in 2020, maar schiet na 2040 wel door de 1200 grens heen. Dat is het gevolg van de babyboom in 1946. Over enkele decennia zal deze lijn toch weer terug moeten buigen richting de 1200/100K.

Maar de aanhangers van de “er is geen oversterfte meer” theorie zien hun kwadratische fit (de rode lijn) al in 2032 door deze 1200 grens heen schieten. Sterker nog, door de keuze van een parabool zal deze alleen maar harder gaan stijgen en nooit de 1200 grens meer kunnen bereiken en zal in 2040 al gestegen zijn tot 1600.

We zien in deze grafiek ook dat de 5 coronajaren volgens het Normsterfte model telkens rond de 50 hoger liggen, er is oversterfte. Maar als we kijken naar de kwadratische prognose, dan is de oversterfte in 2023 overgegaan in ondersterfte. Het gevolg van de keuze voor een kwadratisch model.

De Crisis

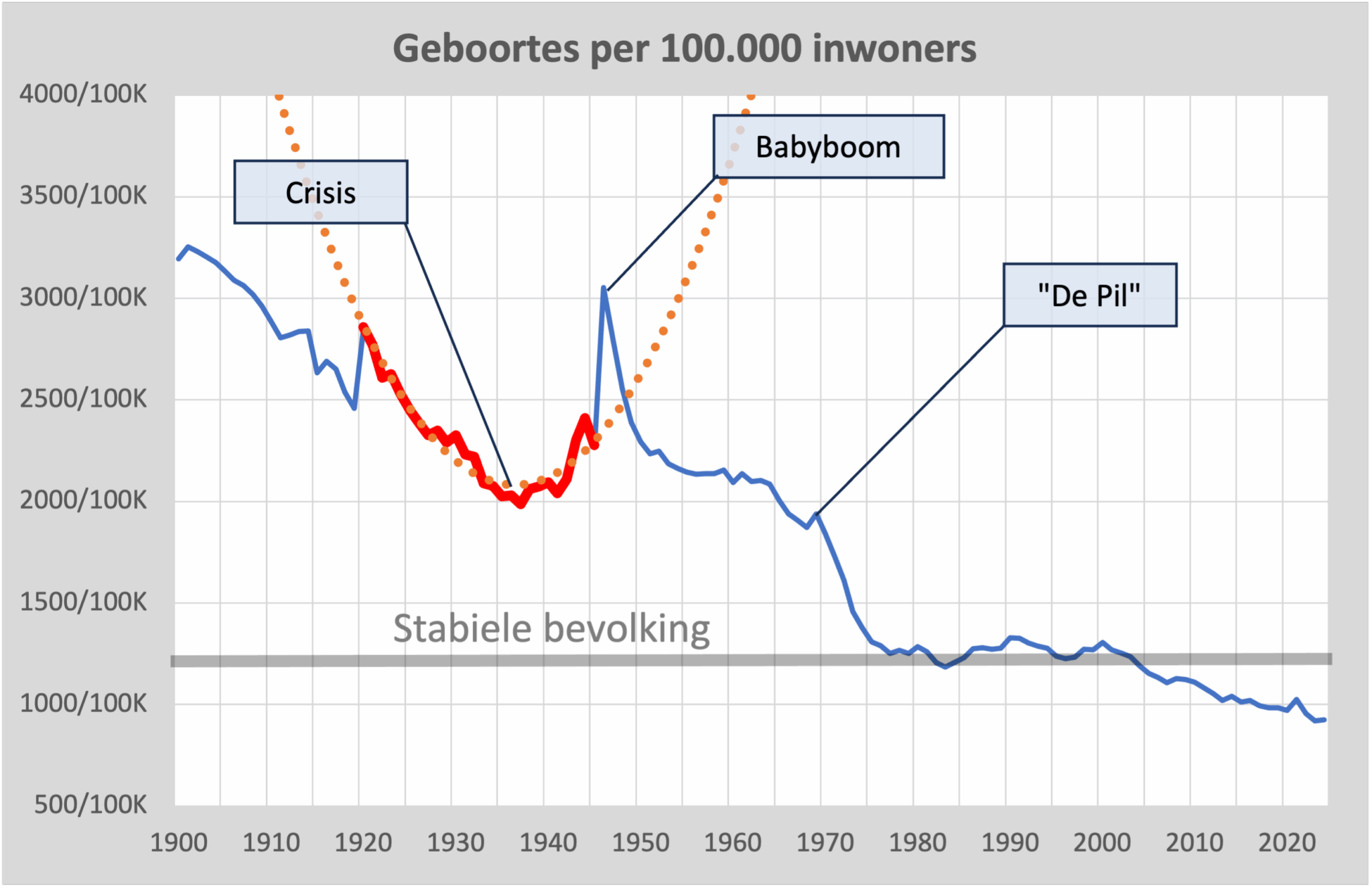De grafiek met het aantal overlijdens per 100K is dus gebaseerd op de verhouding van het aantal overlijdens in relatie tot de gehele bevolking. De lijn volgt dus de opbouw van de bevolking. Maar het aantal overlijdens wordt vooral bepaald door de leeftijden tussen 75 en 85 jaar. Dat zijn dus de mensen die ongeveer 80 jaar daarvoor zijn geboren. Dus de kuil in de sterfte in 2010 moeten we terug kunnen vinden bij de geboortes in 1930.

En dat is dus ook precies wat we zien. Een kuil met een minimum in 1932, de crisisjaren! En pieken na de Eerste en Tweede Wereldoorlog. En een keurige parabool van 1920 tot 1945, precies overeenkomend met de parabool door de jaren 2000-2020. We “fitten” dus de geboortes van 100 jaar geleden! De gevolgen van de bijna halvering van de geboortes na het gratis beschikbaar komen van “De Pil” gaan we dus over enkele decennia zien. Dan zal de sterfte snel gedaald zijn tot rond de 1200/100K.

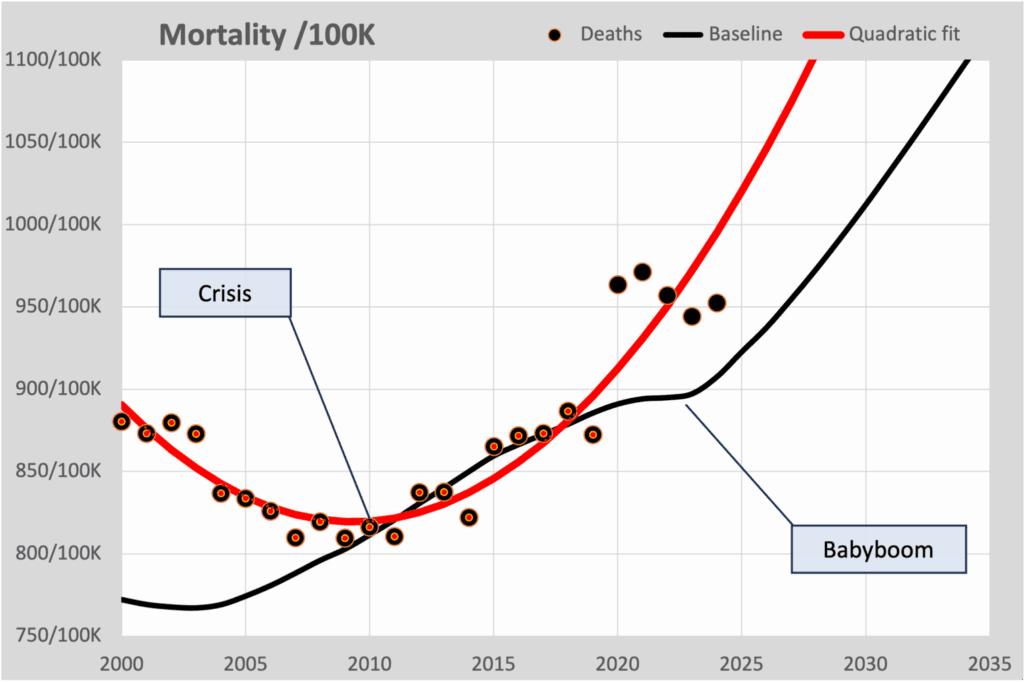We snappen dus nu waar die parabool vandaan komt. We kijken tot 2015 gewoon naar de sterke daling van geboortes tijden de crisisjaren nu honderd jaar geleden. En vanaf 2020 de geboortepiek in 1946 die nu leidt tot verhoudingsgewijs meer sterfte door de vergrijzing.

Het RIVM

Merkwaardig dat ook het RIVM komt met een presentatie waarin cijfermatig dezelfde uitkomst wordt getoond als bij de kwadratische fit: er is volgens RIVM geen oversterfte. Wel is het zo dat het RIVM inmiddels heeft erkend dat hun model helemaal geen langdurige oversterfte kán laten zien. Na het meenemen van ons Normsterfte voorstel, kwam het RIVM met deze brief aan de Tweede Kamer: hun model is ongeschikt voor het vaststellen van langdurige oversterfte. De strekking van deze boodschap lijkt echter niet tot het parlement te zijn doorgedrongen. Maar welke waarde hechten verzekeraars aan de cijfers van het RIVM?

Wat moeten de verzekeraars nu doen?

Verzekeraars zijn gebaat bij een betrouwbare prognose. Als het officiële standpunt zou zijn dat er eigenlijk geen oversterfte meer zou zijn, dan klinkt dat in eerste instantie gunstig. Maar als we even doordenken, dan betekent het dus eigenlijk dat we accepteren dat er een sterk verhoogde sterfte is, die het RIVM nu als “Niet verhoogd” interpreteert. Dus een model dat de huidige sterfte volgt. Laten we dan meteen de kwadratische benadering maar eens meenemen en dan de levensverwachting gaan intekenen.

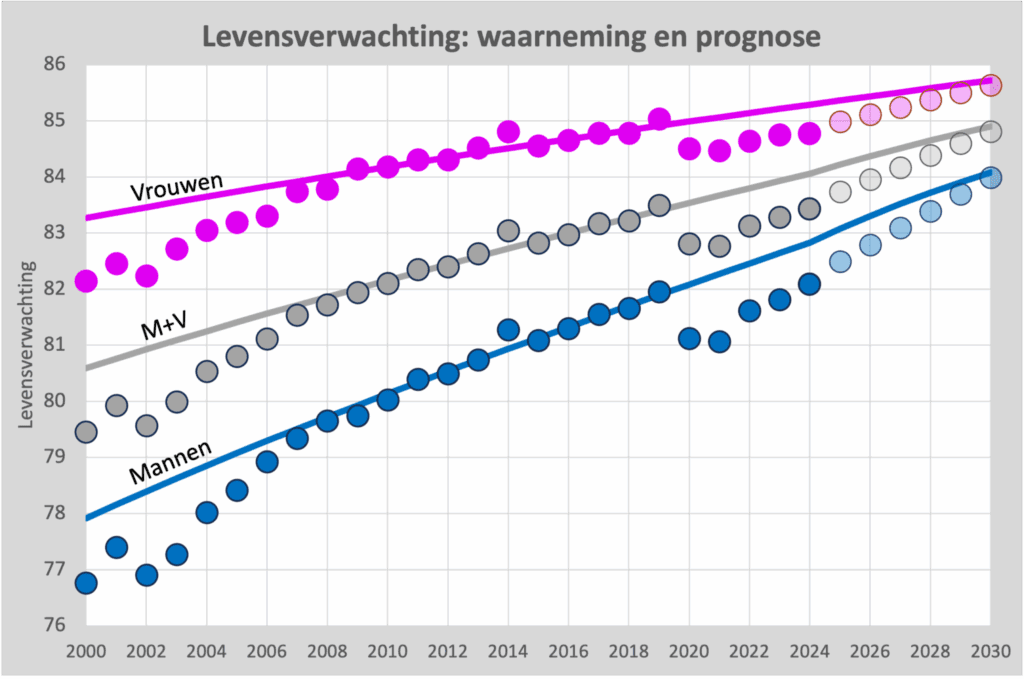
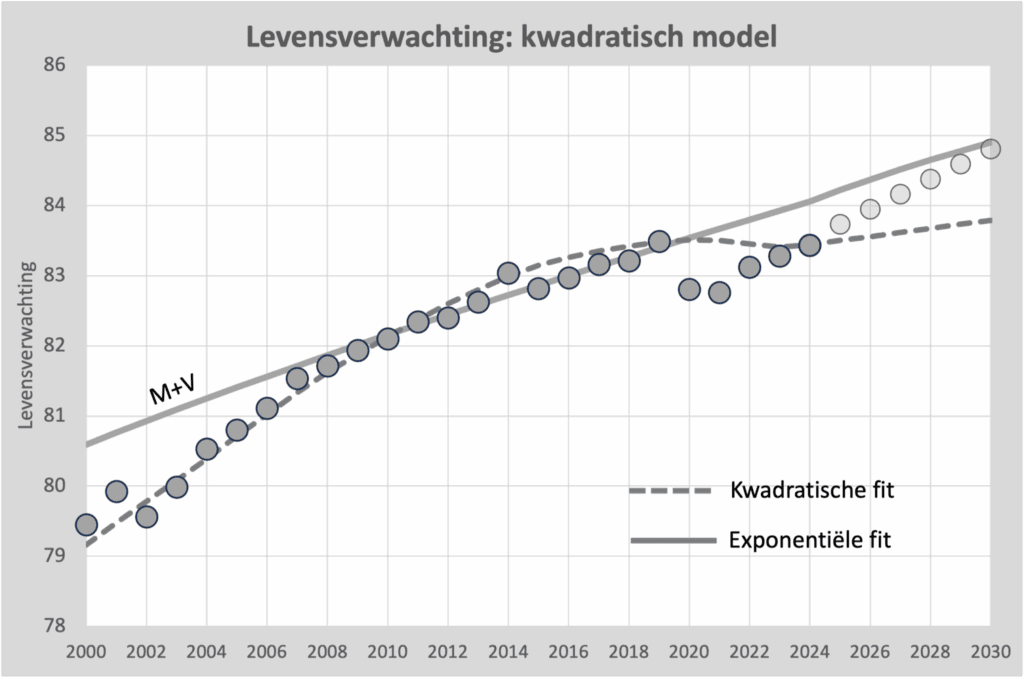In deze grafiek (mannen en vrouwen gecombineerd) zien we weer de werkelijke oversterfte als grijze bolletjes. Dat is dus zoiets als de leeftijd waarbij de helft van de inwoners overleden was. De getrokken lijn is weer de exponentiële fit zoals eerder getoond. In 2020 een daling van 0,7 jaar wegens corona en in 2021 0,9 jaar, vanwege “iets anders”. Vanaf 2022 zien we herstel. Of dat vanaf 2025 verder zal herstellen, is de vraag.

Het kwadratische model (grijze streepjeslijn) ziet iets heel anders. We moeten nu de ligging van de bolletjes vergelijken met deze streepjeslijn. Vanaf 2024 duikt deze lijn onder de werkelijke levensverwachting: de werkelijke levensverwachting is dan hoger dan verwacht! Als we deze lijn dus als “te verwachten levensverwachting” gaan gebruiken, dan komen we bedrogen uit, want we gaan beduidend langer leven en de pensioenpotten raken sneller leeg dan we dachten. Het verschil is vanaf 2023 al boven de 5%  premieverlaging opgelopen. Vanaf 2030 zouden we dan met 10% premieverlaging te maken krijgen.

En ja, wat moeten de verzekeraars nu doen? Wij hebben niet de illusie dat aan ons een advies wordt gevraagd. De pensioenverzekeraars hebben hun premie al aangepast met de vaste indexering. Dit wijst erop dat zij meer vertrouwen hebben in de sterfteprognose zoals het CBS dat vroeger deed en wij nu via onze Normsterfte, dan op de cijfers die het RIVM nu publiceert.

Dus nee, geen daling van de premie te verwachten, de verzekeringen gaan ook uit van een lange termijn prognose, gebaseerd op de trend van voor 2020. De beweringen van zowel RIVM als andere modelleurs dat er geen oversterfte zou zijn, laten zij links liggen. Lees hierover ook bv Een economische verklaring voor de afwijzing van de normsterfte.